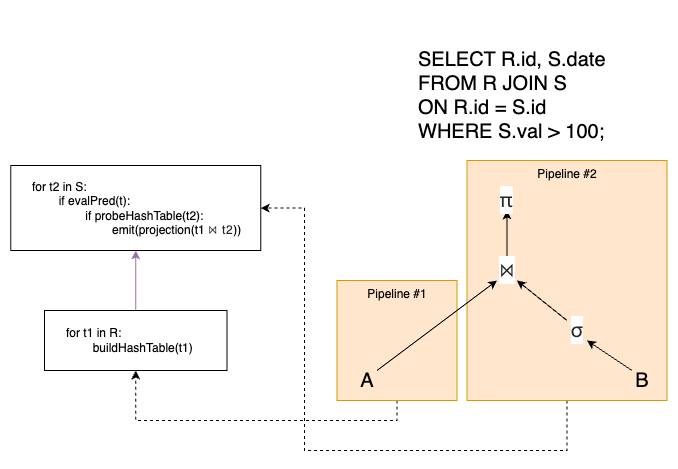
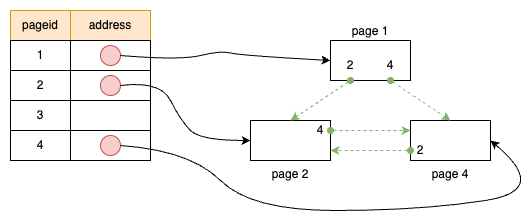
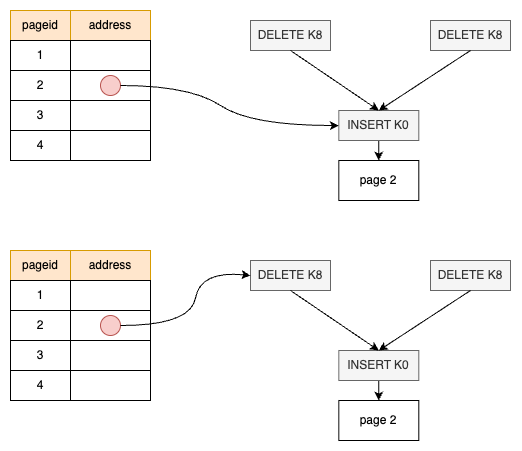
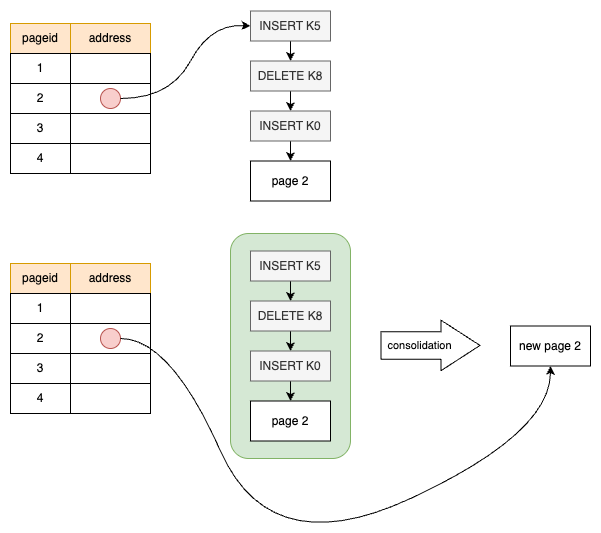
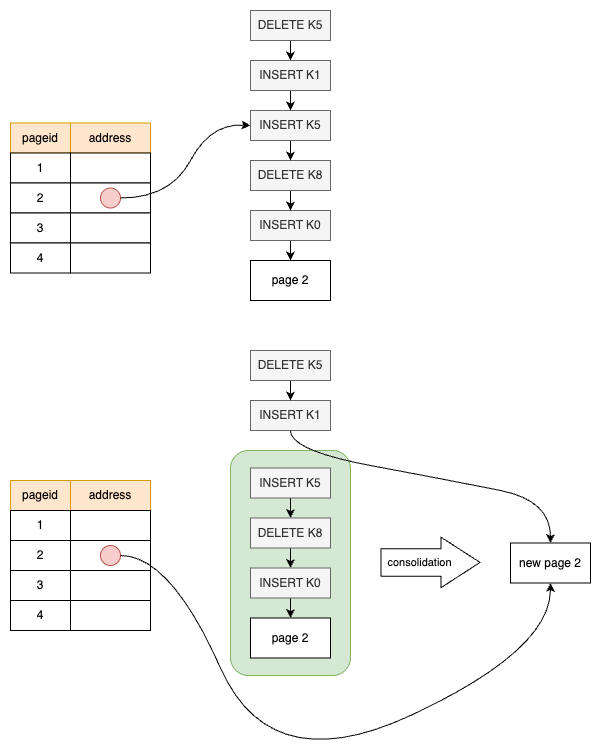
查询优化是构建高性能数据库管理系统时最困难的部分之一,它需要在大量等价的查询执行方案中找到资源消耗最小的那个方案。其核心目标是以某种成本函数衡量每个候选计划,并选择估算成本最低的计划。
查询优化的首要目标就是在可行的计划中选出“最低成本”的一个,通常采用成本模型对 I/O、CPU、网络等资源进行加权求和,得出一个标量成本值,不同系统也可能纳入缓冲区命中率、并行度等额外因素。
成本评估 在关系型数据库的**代价优化器(Cost-Based Optimizer)**中,会将一个查询计划的总代价定义为其所有算子(Operator)估算代价的累加:
C o s t o f P l a n = ∑ ( C o s t o f e a c h P l a n O p e r a t o r )
Cost\:of\:Plan = \sum (Cost\:of\:each\:Plan\:Operator)
C o s t o f P l a n = ∑ ( C o s t o f e a c h P l a n O p e r a t o r ) 而每个算子的估算代价又通常与该算子所处理的输入规模成正比:
C o s t ( O p e r a t o r ) ∝ S i z e o f O p e r a t o r I n p u t
Cost(Operator) \propto Size\:of\:Operator\:Input
C o s t ( O p e r a t o r ) ∝ S i z e o f O p e r a t o r I n p u t 以上两条公式构成了代价估算的基础:先通过输入规模得出算子代价,然后累加得到整个执行计划的成本。接下来,需要详细说明如何确定算子输入规模,以及如何基于选取性(Selectivity)估算非基表算子的输出规模。
对于基表扫描(Table Scan)或索引扫描(Index Scan),输入规模通常等于表或索引在磁盘上的物理存储量(页数或行数)。
[!NOTE]
对于此类扫描操作,我们可以在有索引的情况下,可将过滤条件下推至索引层,只读取满足谓词的行或页,以减少输入规模和 I/O 操作,也就是进行索引下推。
对于投影(Project)、选择(Filter)等算子,优化器首先根据输入规模和选取性估算输出规模;连接(Join)算子则需基于两侧子计划的输出规模与连接选取性共同计算其输出规模,也就是:
O u t p u t S i z e = S e l e c t i v i t y × ( ∣ L e f t ∣ × ∣ R i g h t ∣ )
Output\:Size = Selectivity \times (|Left| \times |Right|)
O u t p u t S i z e = S e l e c t i v i t y × ( ∣ L e f t ∣ × ∣ R i g h t ∣ ) 选取性(Selectivity)是算子发出数据量与接收数据量之比,取值范围 0–1,表示谓词或连接条件对数据的过滤强度。
O u t p u t S i z e = S e l e c t i v i t y × I n p u t S i z e
Output\:Size = Selectivity \times Input\:Size
O u t p u t S i z e = S e l e c t i v i t y × I n p u t S i z e 假设我们针对有 100 条记录的部门表 dept,10000 条记录的职员表 emp,30000 条记录的儿童表 kids,执行如下 SQL 语句:
1 2 3 4 5 SELECT * FROM emp, dept, kidsWHERE sal > 10000 AND emp.dno = dept.dno AND emp.eid = kids.eid;
其中,每 100 条记录是一个页面,10 KB 是一个页面的大小,内存大小是 10 个页面。
对于每种执行计划,我们可以进行如下步骤:
第一步,评估表(关系)的大小:
dept 只有 100 条记录,占用 1 页(10 KB/页);
emp 有 10000 条记录,占用 100 页(10 KB/页);
kids 有 30000 条记录,占用 300 页(10 KB/页)。
第二步,评估选择性:
WHERE sal > 10k 的选择性为 0.1;dept 和 emp 的 JOIN 操作的选择性为 0.01,产生结果集 A;
A 和 kids 的 JOIN 操作的选择性为 0.0001,产生结果 B。
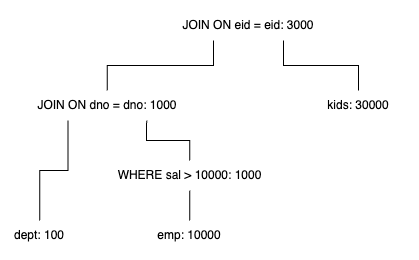
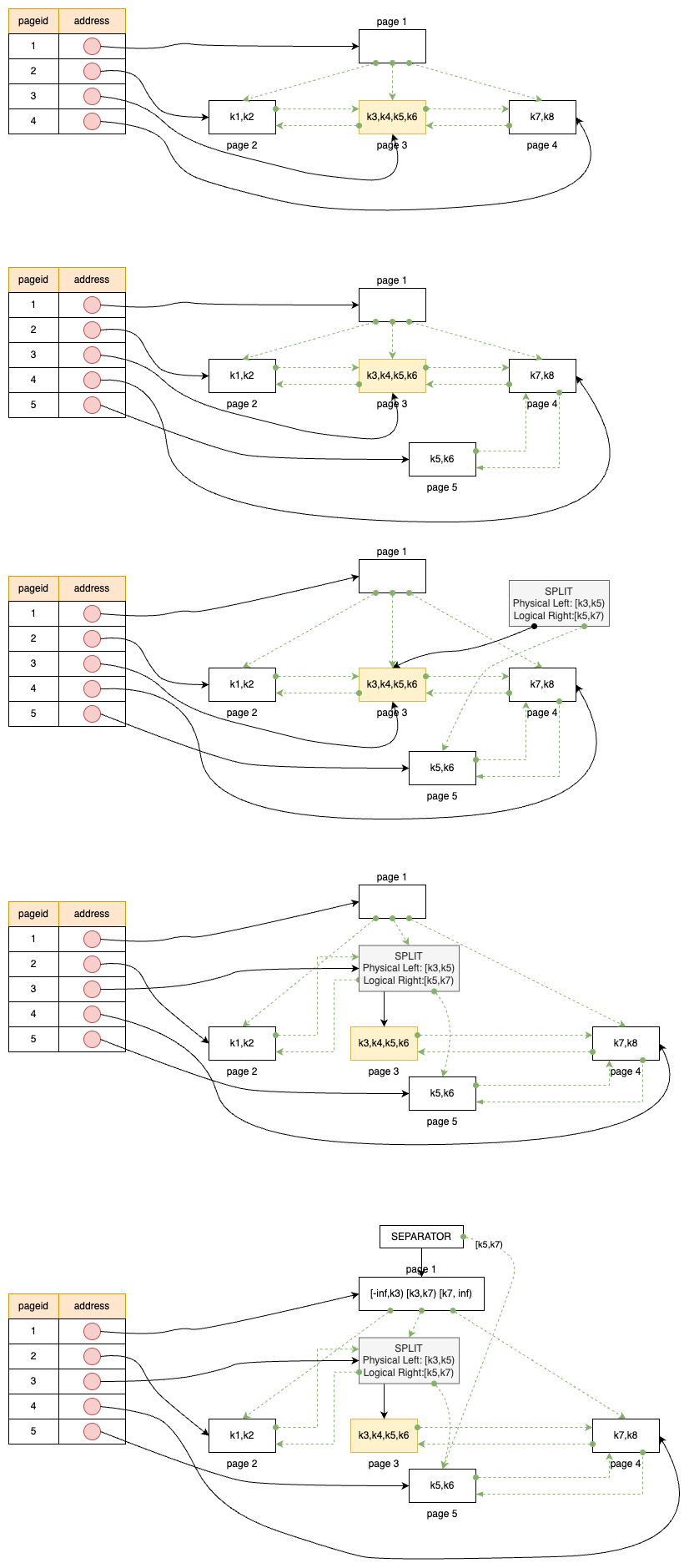
第三步,计算中间结果的大小,如下执行计划树所示,其中冒号右边的数据为此次操作得到的结果集的大小:
需要注意的是,整棵树的阅读顺序推荐从叶子到根。
第四步,评估各个执行计划的成本并选出最低的。
以上只是一个简单的流程,下面基于 Selinger 等人提出的 System R 成本优化器框架给出每个步骤的详细解释,该框架迄今仍被主流关系型数据库(如 DB2、PostgreSQL、MySQL 等)沿用。
第一步,评估关系的大小,其中的统计量如下:
NCARD(T) :关系 T 的基数,即元组总数;TCARD(T) :关系 T 所占用的数据页数;ICARD(I) :索引 I 中不同键值的数量;NINDX(I) :索引 I 在磁盘上占用的页数。
[!NOTE]
现代数据库在 System R 的统计量基础上引入多种增强策略:
直方图(Histograms)
等宽直方图(Equi-width) :将值域划分为固定宽度的 k 个区间,区间内数据不均匀时易失真 。等深直方图(Equi-depth) :保证每个桶内的元组数近似相同,可更准确估算范围谓词 。
最常见值列表(Frequency List) :维护出现频率最高的 m 个键值及其频率分布,对高频值谓词(如 col IN (…))提供精确估算。
聚簇因子(Clustering Factor) :描述索引键值在数据块中的物理聚集度,值越低表示更紧密的簇集,有助于优化随机 vs 顺序 I/O 的成本估算。
分区增量统计 :对于分区表,会为每个分区单独收集统计信息,并维护全局统计,通过分区修剪(Partition Pruning)显著降低查询开销。
分层采样 :在全表采样成本过高时,数据库可基于分区或分层样本抽样(如 1% 分区样本),动态更新统计,同时避免全表扫描统计带来的停机与高 I/O 负载。
第二步,评估选择性:
我们这里先定义 F 或者 F(pred) = 谓词的选择性 = 没有被过滤掉的记录的占比。
那么,对于等值谓词 col == val:若有索引,则假设均匀分布,选取性
F = 1 / I C A R D
F = 1 / ICARD
F = 1 / I C A R D ;否则粗略取 1/10。
对于范围谓词 col > val 或类似开区间比较:若有索引,则线性插值计算
F = ( h i g h _ k e y − v a l ) / ( h i g h _ k e y − l o w _ k e y )
F = (high\_key\:-\:val) / (high\_key\:-\:low\_key)
F = ( h i g h _ k e y − v a l ) / ( h i g h _ k e y − l o w _ k e y ) ;否则取 1/3。
对于列间相等谓词 col1 = col2:
若两列均有索引,取两索引基数(ICARD)较大值的倒数:
F = 1 max ( I C A R D ( c o l 1 ) , I C A R D ( c o l 2 ) )
F = \frac{1}{\max\bigl(\text{ICARD}(col_1),\,\text{ICARD}(col_2)\bigr)}
F = max ( I C A R D ( c o l 1 ) , I C A R D ( c o l 2 ) ) 1 ;
若只有单列有索引,则
F = 1 / I C A R D
F = 1/ICARD
F = 1 / I C A R D ;否则取 1/10。
此外,在查询中常有多重谓词组合,Selinger 优化器使用以下规则在逻辑优化 和成本估算 阶段快速合成最终选取性 F:
逻辑与(AND) :
F a n d = F ( p 1 ) × F ( p 2 )
F_{\text{and}} = F(p_1)\,\times\,F(p_2)
F a n d = F ( p 1 ) × F ( p 2 ) 逻辑或(OR) :
F o r = 1 − F a n d = F ( p 1 ) + F ( p 2 ) − F ( p 1 ) F ( p 2 )
F_{\text{or}} = 1 - F_{\text{and}} = F(p_1) + F(p_2) - F(p_1)\,F(p_2)
F o r = 1 − F a n d = F ( p 1 ) + F ( p 2 ) − F ( p 1 ) F ( p 2 ) 逻辑非(NOT) :
F n o t = 1 − F ( p )
F_{\text{not}} = 1 - F(p)
F n o t = 1 − F ( p ) 思考:
为什么等值谓词在没有索引的时候要取 1/10?
在缺乏精确统计时,优化器宁可假设谓词对数据的过滤效果较弱 (即选取性估算偏大),也不轻易假设它过滤得非常彻底。
如果低估谓词效果(认为它能过滤掉更多行),某些访问路径(如索引扫描)看起来成本极低,以至于优化器可能跳过对其他方案的评估;而高估则保证几乎所有可行方案都被保留用于比较,从而不至于因估算过于乐观而错过实测可能更优的计划。
假设有两种访问 emp 表的方案:
索引扫描+连接 :若低估谓词效果(认为只过滤 1%),算出极低的中间行数,导致优化器只评估此方案并剪掉全表扫描方案。高估策略 (假设过滤 10%):使得索引扫描方案看起来代价更高,全表扫描的成本也被评估,优化器才会真正比较两者。
最终在实际运行中,全表扫描+哈希连接可能因顺序 I/O 更快而胜出,但若一开始就剪掉它,就永远不会被考虑。
第三步,计算中间结果的大小,该步骤的内容之前已经叙述过。
第四步,评估每个执行计划的成本:
在基于成本的优化器中,每个物理算子的总代价通常由以下两部分构成:
I/O 代价 :以读取页面的次数为单位,乘以相应的 I/O 权重(如顺序读取 seq_page_cost 或随机读取 random_page_cost) 。CPU 代价 :以处理记录或执行谓词的次数为单位,乘以对应的 CPU 权重(如 cpu_tuple_cost、cpu_operator_cost) 。
最终,优化器对算子代价取页读次数与记录处理次数的线性组合来估算:
C o s t = ( p a g e s r e a d ) + W × ( r e c o r d s e v a l u a t e d )
\text{Cost} = (\text{pages read}) + W \times (\text{records evaluated})
C o s t = ( p a g e s r e a d ) + W × ( r e c o r d s e v a l u a t e d ) ,其中 W 表示单位记录的 CPU 权重 。
对于带唯一索引的等值谓词 ,访问路径通常为:
B-Tree 索引查找 :读取根到叶的路径上若干索引页(假设固定深度),通常记为 “1 页 I/O” 来表示一次查找操作的近似代价。堆表行定位 (Heap File lookup):利用索引返回的行定位信息,再读取对应数据页,平均也是一次 I/O 操作。
综合起来,此算子的总代价可表示为:
1 ( i n d e x p a g e r e a d ) + 1 ( d a t a p a g e r e a d ) + W ( C P U )
1\ (\text{index page read}) \;+\; 1\ (\text{data page read}) \;+\; W\ (\text{CPU})
1 ( i n d e x p a g e r e a d ) + 1 ( d a t a p a g e r e a d ) + W ( C P U ) 。
该模型假设索引组织为聚簇或近似聚簇结构,因此每次索引查找可定位到唯一一条记录。
对于聚簇索引的范围扫描 ,算子需扫描多个索引条目并可能访问多条数据行,I/O 代价 为
F × ( N I N D X + T C A R D )
F \times (\text{NINDX} + \text{TCARD})
F × ( N I N D X + T C A R D ) ,CPU 代价 为
W × ( t u p l e s r e a d )
W \times (\text{tuples read})
W × ( t u p l e s r e a d ) ,因此整体成本为:
F × ( N I N D X + T C A R D ) + W × ( t u p l e s r e a d )
F \times (\text{NINDX} + \text{TCARD}) + W \times (\text{tuples read})
F × ( N I N D X + T C A R D ) + W × ( t u p l e s r e a d ) ,其中 NINDX 为索引页数,TCARD 为表的总页数,F 为谓词选取性;每个匹配索引条目对应一次数据页顺序 I/O。
对于非聚簇索引的范围扫描 ,CPU 成本和聚簇索引的一致,但是 I/O 成本为
F × ( N I N D X + N C A R D )
F \times (\text{NINDX} + \text{NCARD})
F × ( N I N D X + N C A R D ) ,因此整体成本为:
F × ( N I N D X + N C A R D ) + W × ( t u p l e s r e a d )
F \times (\text{NINDX} + \text{NCARD}) + W \times (\text{tuples read})
F × ( N I N D X + N C A R D ) + W × ( t u p l e s r e a d ) ,此时每个匹配条目都可能落在不同的数据页上,平均需一次随机 I/O,因此用 NCARD(行数)来近似页数。
对于分段顺序扫描 ,不利用索引,需读取表的所有页并评估所有行:
C o s t = T C A R D + W × N C A R D
\text{Cost} = \text{TCARD} + W \times \text{NCARD}
C o s t = T C A R D + W × N C A R D ,其中 TCARD 为全表页数,NCARD 为元组总数;顺序扫描的 I/O 可享有预取(prefetch)与缓冲优势,故只计算页面读取的总数。
接着,我们来看 JOIN 的成本计算,以嵌套循环连接 (Nested-Loop Join)为例。
它的总代价公式 :
C o s t N L J ( A , B ) = C o s t ( A ) + N C A R D ( A ) × C o s t ( B )
\mathrm{Cost}_{\text{NLJ}}(A,B) = \mathrm{Cost}(A) \;+\;\mathrm{NCARD}(A)\times \mathrm{Cost}(B)
C o s t N L J ( A , B ) = C o s t ( A ) + N C A R D ( A ) × C o s t ( B ) ,其中 A 为外层计划,B 为内层基表,NCARD(A) 为外层输出元组数。
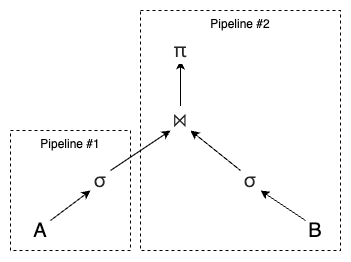
为了控制连接顺序的枚举复杂度,System R 优化器仅考虑左深树 :
每一步连接的右子树 B 必须为尚未使用的基表,而非先前连接出的中间子树。
这样能保证枚举过程中只需维护基表之间的累积连接,而无需考虑更复杂的树形拓扑,大幅减少计划数量(从 $O(N!)$ 降到约 $O(2^N)$)。
[!NOTE]
之前例子中的图就是一棵左深树。
对于谓词形如 B.key = A.key,且在 B 的 key 列上存在唯一或聚簇索引 ,优化器近似认为:
一次 B+Tree 索引查找需 “1 页” I/O(从根到叶路径平均代价)。
根据索引返回的行定位信息,再一次 Heap File lookup 也需 “1 页” I/O。
最后对该行执行谓词或投影等操作,产生 W 单位的 CPU 代价。
综合得到:
C o s t ( B ) = 1 + 1 + W
\mathrm{Cost}(B) = 1 \;+\; 1 \;+\; W
C o s t ( B ) = 1 + 1 + W ,该模型忽略了缓存预取及并行扫描等复杂因素,但其简洁性足以支撑海量计划的快速比较。
若内层无可用索引,则只能顺序扫描整个表:
因此:
C o s t ( B ) = T C A R D ( B ) + W × N C A R D ( B )
\mathrm{Cost}(B) = \mathrm{TCARD}(B)\;+\;W\,\times \mathrm{NCARD}(B)
C o s t ( B ) = T C A R D ( B ) + W × N C A R D ( B ) ,该模型同样简化了缓冲与批量读写等优化手段,但体现了顺序扫描的典型开销。
如果是 Sort-Merge Join 的话,代价模型:
C o s t = C o s t ( A ) + C o s t ( B ) + s o r t c o s t
Cost = Cost(A) + Cost(B) + sort\:cost
C o s t = C o s t ( A ) + C o s t ( B ) + s o r t c o s t
Cost(A) :外层子计划(子树)A 的总代价;Cost(B) :内层子计划 B(可以是基表或中间结果)的总代价;sort cost :对 A 和 B 各自执行排序的代价之和。
排序—归并连接是一种基于将两输入关系各自按连接键排序,随后线性归并扫描输出匹配对的算法。
阶段一:排序(Sort)
对输入关系 A、B 按连接属性(pred 中指定的字段)各自进行排序。
如果输入已经部分或完全有序,则可跳过或简化排序步骤。
阶段二:归并(Merge)
维护两个游标,分别指向 A、B 的当前最小键值记录。
比较当前 A、B 键值:
若 A.key < B.key,则将 A 游标前移;
若 A.key > B.key,则将 B 游标前移;
若相等,则输出所有相同键值的配对(可能需要在一个输入保留缓冲区中暂存重复键值),并前移游标。
该归并过程只需一次顺序扫描,两边各推进,故 I/O 和 CPU 都相对高效。
适用场景
两输入均可顺序访问或已排序,且连接键上无合适哈希索引时最优;
特别适合大批量数据输出且需要顺序结果的场景。
如果后续操作涉及选取最大最小值,那么最好使用 Sort-Merge Join 先得出排序后的 JOIN 结果。
第五步,选出成本最低的执行计划:
若对所有可能的联接树与交叉产品一一枚举,计划数目将呈阶乘级增长,无法承受 。System R(Selinger 优化器)的核心思想是,通过启发式剪枝 大幅减少搜索空间,同时用自底向上动态规划 保证在受限空间内选出最优左深计划。
全空间规模 :对 n 个基表,所有可能的联接树数约为 n!(叶深树)。例如 6 表联接时有 6! = 720 种联接顺序;10 表时增至 3 628 800 种。启发式目标 :在保证生成足够优质计划的前提下,剪掉绝大多数计划,避免枚举交叉组合、子查询作为内层的树形连接等无效情况。
这里展示三大启发式规则 :
谓词下推
越早执行过滤谓词,可最大程度减少后续算子的输入规模与 I/O 或 CPU 代价。
在构建执行计划时,把每个谓词 $\sigma$ 尽可能下推到最接近基表扫描或索引扫描的层面,不把过滤延迟到后面再算。
避免笛卡尔积
对无关联谓词的表进行笛卡尔积会产生极大中间结果,通常不可接受。
仅在所有过滤条件均已消耗殆尽 (即查询本质需要交叉连接)时,才枚举产生交叉产品的计划;否则只枚举带有有效联接谓词的表对。
仅枚举左深树
在左深树中,每次联接的右子树必须是一个基表 ,而不能是先前联接所得的中间子树。
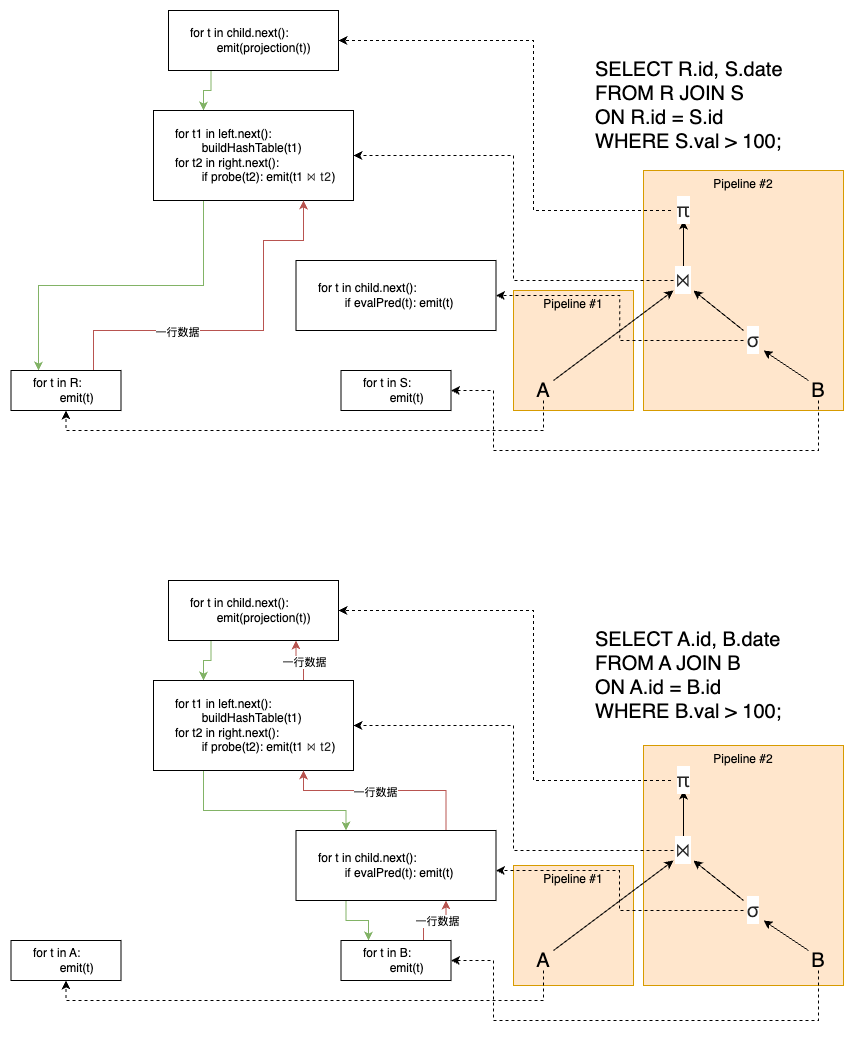
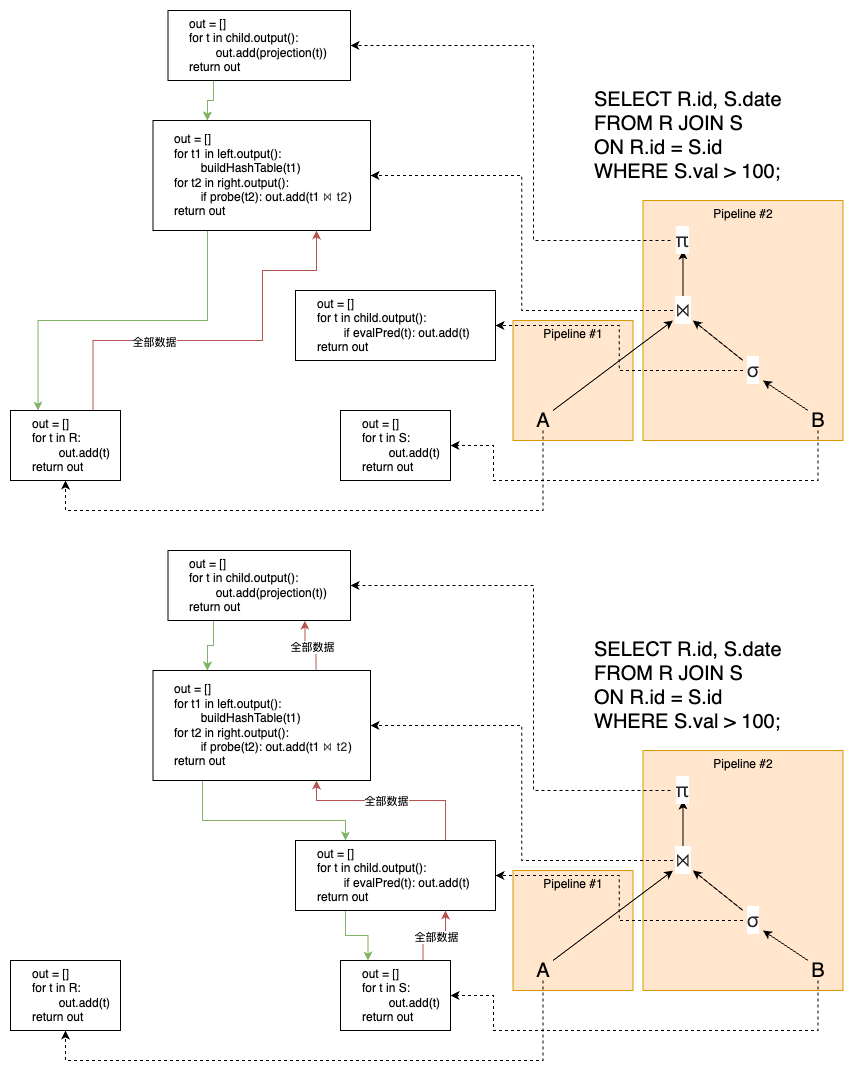
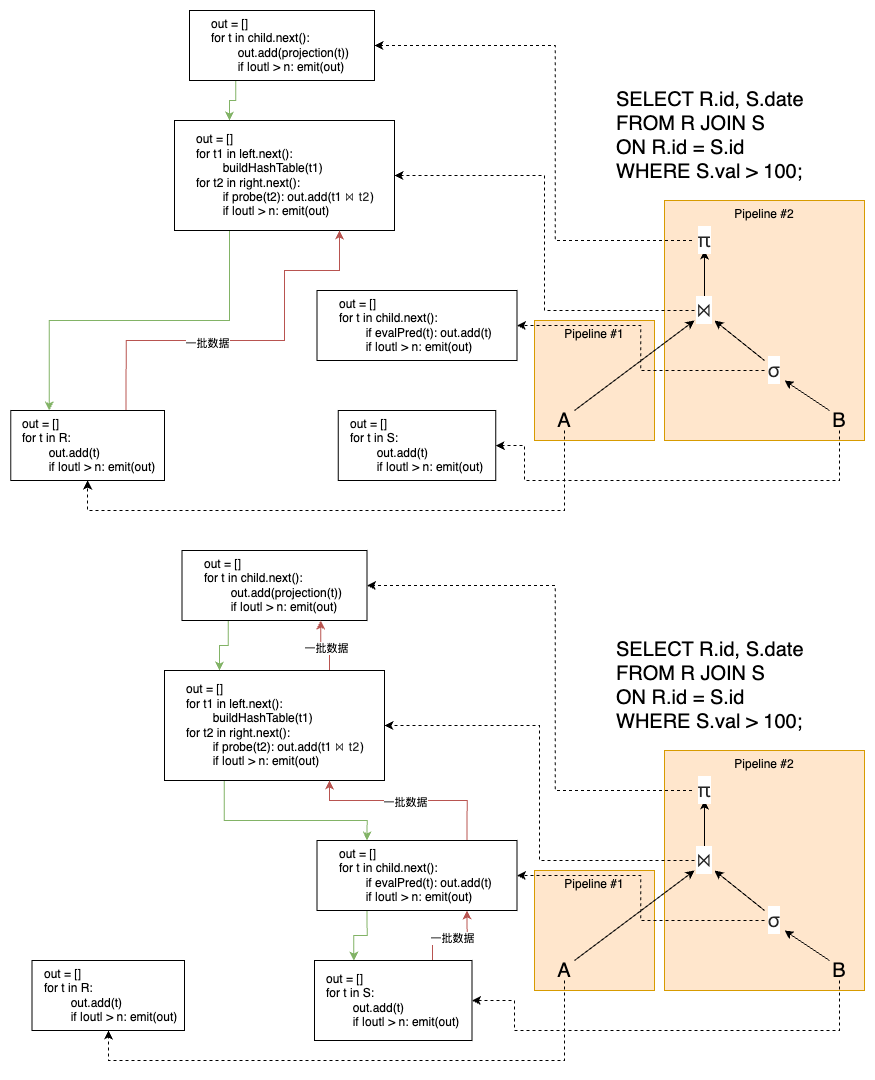
这样可以使得搜索空间大幅缩减 :从全空间的 O(n!) 降至约 O(2ⁿ) 或更小;以及流水线执行 :左深树可实现完全流水线(pipelining),中间结果无需写入磁盘临时表;对大多数算子(NLJ、Hash Join、Merge Join)均适用。
自底向上的动态规划
以上的三种启发式规则带来的提升有限,所以 System R 还引入了动态规划。
动态规划算法利用了最优子结构 的性质:如果在所有包含关系集 {A,B,C} 的计划中,连接 A、B、C 最优的顺序是 (A ⋈ B) ⋈ C,那么无论这个三表子集在更大计划中如何出现,(A ⋈ B) 必然是 {A,B} 的最优子计划之一,不需要再次枚举.
由于子计划不依赖于外部上下文,其最优性是全局性的,只需计算一次,即可复用到所有包含该子集的更大计划中。这一思想即 “不要在更大的计划中重新考虑子计划”。
System R 优化器按照子计划包含的基表数目,从小到大分层枚举:
第 1 轮 (1-表计划):分别为每个基表 $R_i$ 选择成本最低的访问路径(全表扫描或索引扫描)并记录其成本与输出行数。第 2 轮 (2-表计划):对第 1 轮中的每个单表计划 P(作为外层),将尚未使用的每个基表 $R_j$ 作为内层,计算连接成本,并在所有方案中保留最优者。… 第 k 轮 (k-表计划):对所有包含 k-1 表的最优子计划 S,尝试将每个剩余基表 R 连接进来,更新并保留每个大小为 k 的子集的最优左深计划,直至包含所有 n 张表。
如此,算法以 n 轮完成枚举,每轮仅对上一轮的最优子计划进行扩展,不必遍历所有 O(n!) 种联接树,空间和时间复杂度可控制在指数级但远低于阶乘级别。
用伪代码来表示就是:
1 2 3 4 5 6 7 8 9 10 11 12 13 R ← set of relations to join for i in {1 …|R|}: for S in {all subsets of R of size i}: optcost_S = ∞ optjoin_S = ∅ for a in S: c_sa = optcost_{S–{a}} + min_cost_to_join((S–{a}), a) + min_access_cost(a) if c_sa < optcost_S: optcost_S = c_sa optjoin_S = optjoin_{S–{a}} ⨝ a
该算法默认只搜索左深树,因为可以在子集拆分的时候采用 S - a + a 的方式来选取已有的子树和要 JOIN 的基表,并大幅减小搜索空间。
以 PostgreSQL 中的最优子计划复用为例:
1 2 3 4 5 6 Hash Join (cost= 347292.59 ..498019 .60 rows = 3000001 width= 36 ) Hash Cond: (kids.eno = emp.eno) - > Seq Scan on kids (cost= 0.00 ..49099 .01 rows = 3000001 width= 18 ) - > Hash (cost= 163696.15 ..163696 .15 rows = 10000115 width= 22 ) - > Seq Scan on emp (cost= 0.00 ..163696 .15 rows = 10000115 width= 22 )
1 2 3 4 5 6 7 8 9 Hash Join (cost= 350376.61 ..556245 .96 rows = 3000001 width= 40 ) Hash Join (cost= 347292.59 ..498019 .60 rows = 3000001 width= 36 ) Hash Cond: (kids.eno = emp.eno) - > Seq Scan on kids - > Hash - > Seq Scan on emp - > Hash (cost= 1443.01 ..1443 .01 rows = 100001 width= 8 ) - > Seq Scan on dept
假设有四个表 A、B、C、D,它们通过动态规划选出最优执行计划的步骤如下:
当前计算出 A 的最优执行计划是索引扫描,B 是顺序扫描(C 和 D 这里不展示),那么 {A, B} = AB or BA,{A, C} = AC or CA,{B, C} = BC or CB。
经过一系列计算,我们可以在动态规划中得出如下的备忘录:
Relations
Best Plan
Cost
A
Index Scan
5
B
Seq Scan
15
…
…
…
{A, B}
B ⨝ A
75
{A, C}
A ⨝ C
12
{B, C}
C ⨝ B
22
…
…
…
之后,我们要计算 {A, B, C},那么就是要计算:
不包含 A 的:比较 A({B, C}) 和 ({B, C})A;
不包含 B 的:比较 ({A, C})B 和 B({A, C});
不包含 C 的:比较 C({A, B}) 和 ({A, B})C。
这个时候我们发现 {A, B}、{A, C}、{B, C} 的最优执行计划已经被缓存起来了,可以直接复用。perfecto!
最终,我们可以得出如下的备忘录表:
Relations
Best Plan
Cost
A
Index Scan
5
B
Seq Scan
15
…
…
…
{A, B}
B ⨝ A
75
{A, C}
A ⨝ C
12
{B, C}
C ⨝ B
22
…
…
…
{A, B, C}
(CB) ⨝ A
35
{B, C, D}
(CB) ⨝ D
42
…
…
…
{A, B, C, D}
((CB) ⨝ D) ⨝ A
57
因此,我们可以知道 JOIN ABCD 这四个表的最低成本和最优执行计划了。
并且该算法在最差情况下需要枚举所有表子集并对每个子集尝试所有可能的最后加入表,因此具有指数级时间复杂度:O(n · 2ⁿ)。
我们可以将该问题等价成类似 01 子集问题,也就是 n 张表对应一串长度为 n 的二进制串,第 i 位为 1 代表关系 i 已经被 JOIN 了,因此有 2ⁿ - 1 个子集。而且每个子集要进行 n 次状态转移计算,也就是尝试去除集合中的某一个表来构建连接计划。最终两者相乘可得出如上的时间复杂度。
有趣排序(interesting order)
查询优化器在枚举左深执行计划时,除了比较不同访问路径和连接算法的代价外,还要考虑输出结果的排序属性——若某计划天然生成了对后续算子(如 Merge Join、ORDER BY、GROUP BY、去重等)有用的顺序,则称该排序为有趣排序。优化器会为每个子集在每种 有趣排序下各自缓存最优子计划,从而保证后续算子能够直接利用已有排序,避免额外排序或物化开销,但这也会使枚举空间按有趣排序数量 k 成倍增长,总体复杂度增加 k + 1 倍。
尽管枚举空间增加,优化器借此能提前利用排序属性,减少后续全局排序及临时物化,往往在整体查询时间上取得收益,尤其在多级排序或多次归并连接链中更为明显。
1 2 3 4 for each subset S of relations: for each interesting order o in {unordered} ∪ Orders(S): compute min-cost plan producing S with order o keep plan if cost smaller than previous best for (S,o)
基数估算 基数估算(Cardinality Estimation)是成本模型的核心环节,优化器需要对每一种可能的关联操作都进行行数估算;当查询涉及 8–16 张表关联时,由于关联顺序的组合数呈指数级增长,可能需要上百到上千次估算;为了避免优化阶段延迟过大,估算器通常要在毫秒级完成一次估算;因此,各数据库系统普遍采用各种快速而简化的假设或采样策略,在估算精度与执行开销之间做权衡。
PostgreSQL 在 pg_statistic 系统目录中,为表的每一列收集的两大核心统计:
直方图边界(histogram_bounds) :按等频原则划分的区间边界,用于估算范围查询的选择性。最常见值列表(most_common_vals) :出现频率最高的一组值及其对应频率,用于快速处理等值查询。查询优化器在生成执行计划时,会结合这两类统计信息来估算谓词的行数(selectivity),进而比较不同执行策略的成本。
下面将介绍这两种方案。
直方图又分为等宽和等深两种类型:
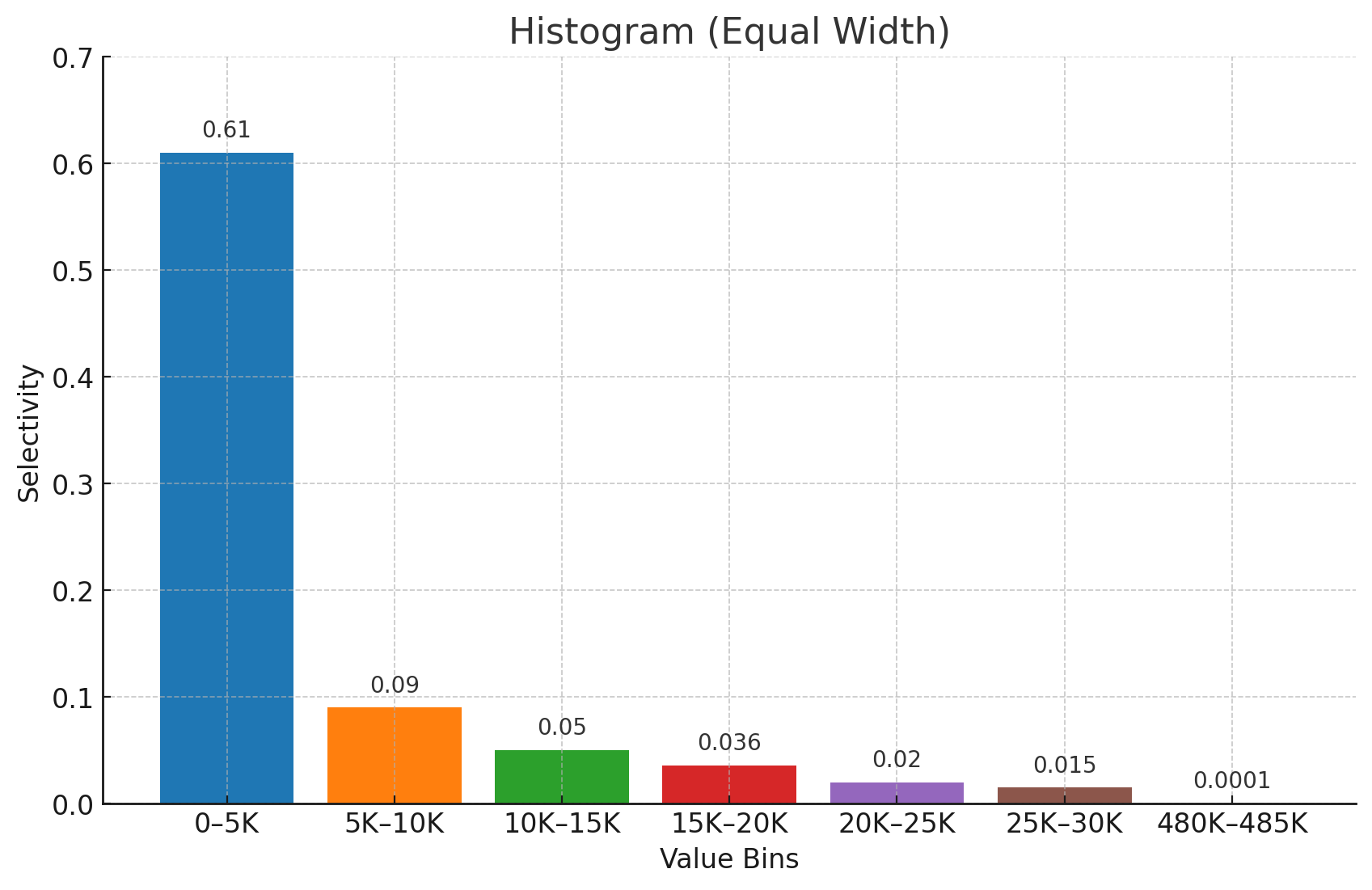
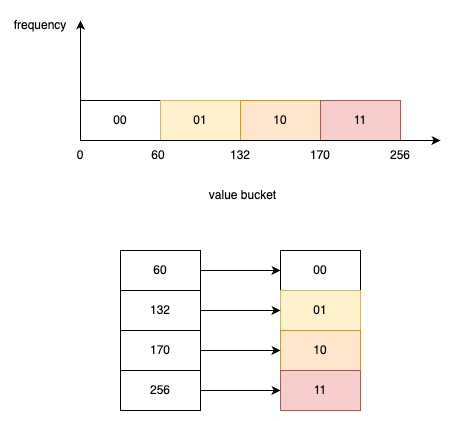
等宽直方图(Equal-Width Histogram)是最简单的直方图类型,它将数据值范围等分成若干个固定宽度的桶(bins),并统计每个桶内数据所占的比例(selectivity)。下图将总共 7854 条记录分入等宽的若干个区间(比如 0–5K、5K–10K 等),并在每个桶上方标注该区间内记录占总量的比例(如 0–5K 桶占 61%)。查询优化器可以利用这些比例估算范围查询或不在最常见值列表中的等值查询的行数,从而评估不同执行计划的成本。
根据上图,如果我们要选取小于 5000 的数据,那么操作的范围只局限于第一个桶中,因此估算的基数为 0.61 * 7854 = 4796。
但这里会有个问题:如果范围查找的数值不是某个同的边界呢?也就是比如我们想查找小于 7500 的数据,而这个值刚好在第二个桶的正中间。这个时候我们只能假设数据为均匀分布,但是实际情况并不总是如此:可能大部分数据都集中在第二个桶的 5-6K 这一部分,也可能集中在 9-10K 这一部分,因此会存在较大误差。同时为了减少误差,我们又不可能无限制地缩小每个桶的宽度,因为最终会导致大量的桶,反而会加剧查询和存储的开销。因此我们需要等深直方图。
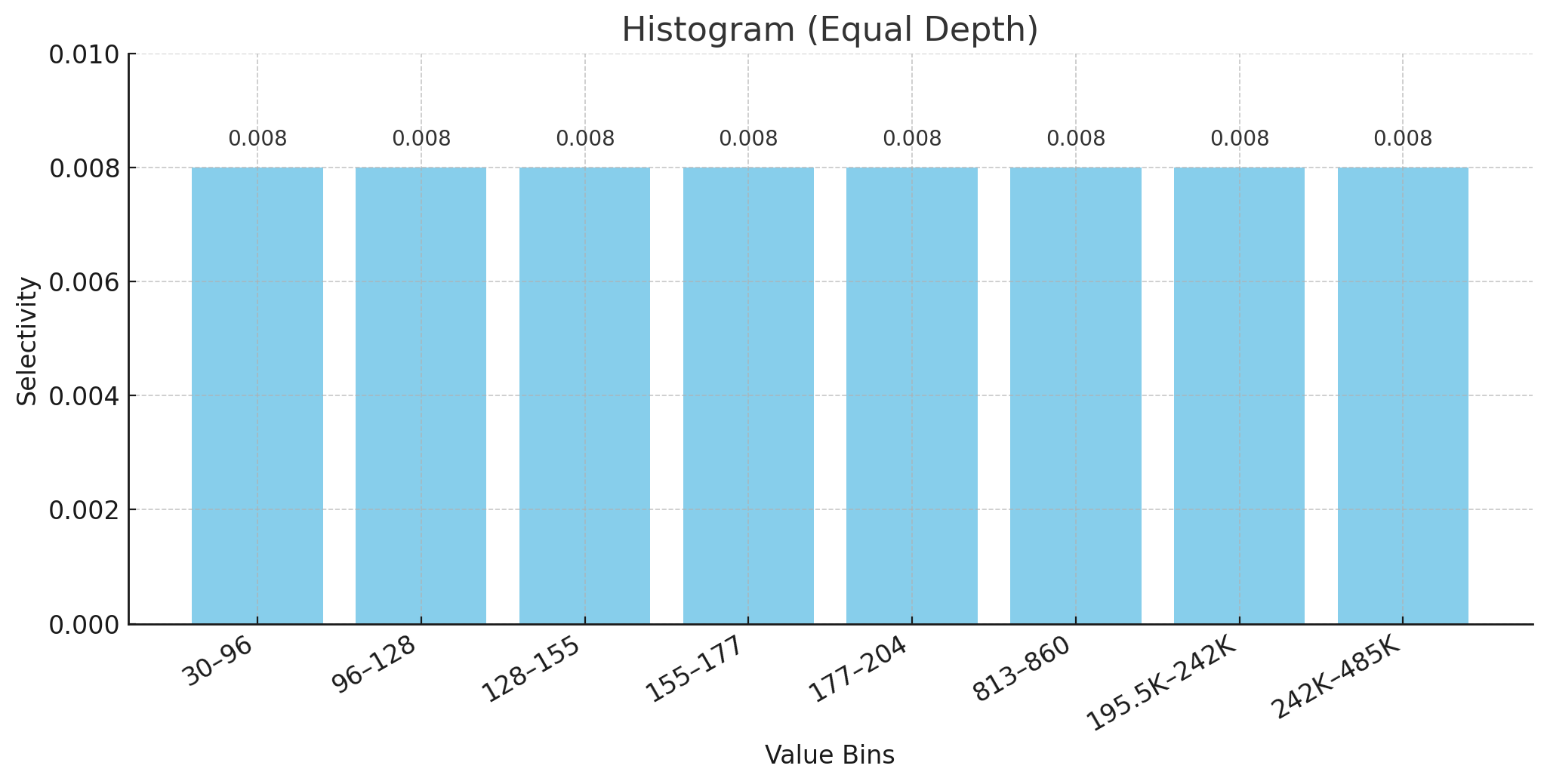
等深直方图(Equal-Depth Histogram)通过保证每个桶内的行数(频数)大致相同 来划分数据范围。下图仍然是针对 7854 条记录使用 100 个桶来划分,每个桶含有相似数量的值,因此即使值域跨度不均,桶高(selectivity)也差不多(≈0.008),更能反映底层数据分布的真实密度。
在上图中,如果我们要选取小于 195.5K 的数据,那么操作范围在最后两个桶中,因此估算的基数为 (0.008 + 0.008) * 7854 =126。
通常来说,等深直方图由于等宽直方图,因为它保证了每个桶的选取性的一致,从而导致数据分布更密集的桶更窄,数据分布更稀疏的桶更宽,这更好地反映出了数据分布。但是这样的维护成本也会更高,尤其是某些 DML 操作导致一个桶的高度变化时,它之后的桶需要不断地移动一些数据到这个桶直到选取性达到 0.008,之后的每个桶需要不断往前一个桶移动数据来保证每个桶的高度达到 0.008,每个桶的在 X 轴上的范围也可能会因此变化,甚至某些情况下的工作量不亚于从头构建。此外,每个桶中的数据倾斜仍然无法被避免。
也就是,如果我们要选取小于 347866 的数据,那么仍然需要假设为均匀分布,这个时候遇到的问题和等宽直方图的是一样的。
通常情况下导致数据倾斜的大概率是一些极端离群值(outliers),我们可以通过下面这个方案来处理它。
等深直方图 + 最常见值(Most Common Values)
这个方案中,对于出现极高频率或明显偏斜的值,等深直方图会将它们剔除到最常见值列表,以免扭曲桶的划分边界和高度。
Value
Selectivity
0
0.07
1
0.0048
2
0.00407
…
…
94
0.0002
850
0.0007
Total 0.14
上面这个表格就是最常见值列表。
如果我们要选取等于 0 的数据,那么直接从最常见值的表里获取 0.07,然后 0.07 * 7854 = 550 就是预估的基数。
如果我们要选取大于 812 且小于 860 的数据,那么估算的基数为 (0.008 + 0.0007) * 7854 = 68.45。
但是这个方案仍然存在问题:当我们对多字段(列)的谓词过滤进行基数预估的时候,往往会低估基数,也就是预估的基数往往会比真实操作的元组的基数要低。这是因为不同列的过滤谓词被假设彼此独立,即联合选择性等于各单列选择性的乘积。这种做法在实际数据分布中往往并不成立:当列之间存在相关性时,单列乘积往往远小于真实的联合选择性,导致估算行数被严重低估,从而可能选择次优的执行计划。
为了克服完全独立性假设在多谓词估算中严重低估结果的问题,SQL Server 引入了三种谓词相关性假设:
完全独立 :各谓词假设互不相关,联合选择性直接相乘。完全相关 :各谓词假设完全相关,联合选择性取最小者。部分相关 :折中假设,既不完全独立也不完全相关,通过对较低的选择性取根号后再相乘,减缓低估程度。
而多列 MCV 是将单列 MCV 的思路扩展到多列组合上:在统计收集阶段,为常一起出现在 WHERE 条件中的列组建立一个联合 MCV 列表,记录这些组合值及其联合频率;查询时,若谓词中出现该组合值,优化器即可直接使用其真实联合选择性,而无需依赖独立性假设或柱状图估算,从而显著提升多谓词过滤的准确性。
balance
age
selectivity
4776
34
0.009
76325
41
0.0005
…
但是这种方案的构建成本会随着查询涉及的列数的增长而增长。
同样,多列直方图也面临多个列的组合的爆炸式增长问题。
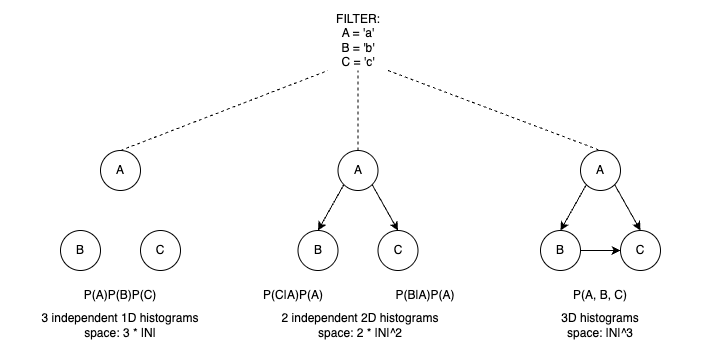
最后一种方案是 BayesCard:传统查询优化器常用独立直方图 ,对每列单独建模并将联合选择性取乘积 P(A)P(B)P(C),这种方法速度极快但在列高度相关时严重低估真实结果;若对多列直接建立三维直方图 ,空间开销将成指数级
O ( ∣ N ∣ 3 )
\mathcal{O}(|N|^3)
O ( ∣ N ∣ 3 ) ,也无法在生产环境中普及。图形模型 (如 Bayesian 网络)通过学习列间条件依赖,并将联合分布因子化为若干局部条件概率:
P ( A ) P ( B ∣ A ) P ( C ∣ A , B )
P(A)\,P(B\mid A)\,P(C\mid A,B)
P ( A ) P ( B ∣ A ) P ( C ∣ A , B ) ,在保留关联性的前提下,将参数规模控制到
O ( 2 ∣ N ∣ 2 )
\mathcal{O}(2|N|^2)
O ( 2 ∣ N ∣ 2 ) ,从而在毫秒级完成联合 Selectivity 推断,并在多项基准测试中显著降低估算误差,实现了精度与性能的平衡。
关于 BayesCard 的具体内容可参考:https://arxiv.org/pdf/2012.14743
传统关系型数据库对等值和范围谓词均有成熟的统计信息(如直方图、最常见值列表)支持,但对于 LIKE 和 UDF 这两类黑箱谓词,数据库优化器往往难以利用现有统计直接估算、只能退而求其次使用启发式规则或假定常数选择性,导致估算误差大、执行计划次优。近年来,研究界针对 LIKE 查询提出了模式/序列模型 (pattern-based 或 positional histograms)来改善精度,而 UDF 则几乎无法通过统计建模,只能依赖运行时采样 或成本抑制 策略。
模式/序列直方图方法
SPH(Sequential Pattern-based Histogram) :通过挖掘字符串的频繁子序列,将常见的子串模式构建成模式直方图,在优化时根据查询模式匹配度快速估算 selectivity,从而显著优于传统直方图和常数假定。
Positional Sequence Patterns :针对 SPH 偶尔会高估的问题,引入位置序列模式区分相邻匹配与可插入匹配,通过信息熵剔除冗余模式,再结合分区匹配策略,使 LIKE 查询的平均误差率降低约 20%。
深度学习方法 :近期有工作利用神经网络对 LIKE 模式进行表征和回归预测,能够学习复杂通配符下的非线性分布,但目前仍处于研究阶段,工业界应用有限。
样本采样(Sampling)
样本采样是一种简单直接的基数估算方法:在数据库中为每张表维护一个小规模的随机样本(例如,1% 的行)并常驻内存;在优化阶段,针对查询谓词仅在样本上执行过滤,计算样本命中率,然后将其外推到全表数据,得到整体选择性和估算行数。
该方案的优点是:
支持任意谓词 :由于直接在样本上运行过滤运算,不依赖预先计算的直方图或分布假设,对任何 运算符或 UDF 都有效。
摆脱独立性等假设 :无需假设列间相互独立,也无需假设值在桶内均匀分布;样本大致反映真实分布,即可获取估算。
易于集成 :只要在优化器中加入样本访问路径,就能在编译阶段快速完成过滤并计算比例,无需维护复杂的统计结构。
缺点是:
可能遗漏极端值 :如果查询谓词对应的行在样本中未出现(例如极端离群值或低频组合),会导致估算为零或极小,严重低估真实行数。
编译时开销 :需要在优化阶段执行过滤运算,若样本量或谓词复杂度较高,编译时间可能显著增加;采样比例若过低,则准确度下降,否则延迟上升。
不适用于多表连接 :在多表连接查询中,需要对多个表的样本进行笛卡尔组合或联动抽样,开销与实现复杂度呈指数级增长,因此通常不对连接 使用样本采样估算,只针对单表谓词有效。
下面展示 PostgreSQL 中是如何进行基数估算的:
PostgreSQL(沿用 System R 的经典做法)对单列等值联结 R₁ ⋈ R₂ ON R₁.a = R₂.a 估算行数时,先分别估算表过滤后行数 |R₁|、|R₂| 及各自该列的基数 (d₁、d₂),然后假定联结属性在两表中同构分布并采用最保守的分母:
∣ R 1 ⋈ R 2 ∣ ≈ ∥ R 1 ∥ × ∥ R 2 ∥ max ( d 1 , d 2 ) .
\bigl|R_1 \Join R_2\bigr| \;\approx\; \frac{\|R_1\|\;\times\;\|R_2\|}{\max(d_1,\,d_2)}.
∣ ∣ R 1 ⋈ R 2 ∣ ∣ ≈ max ( d 1 , d 2 ) ∥ R 1 ∥ × ∥ R 2 ∥ . ,其中 max(d₁,d₂) 是两表中该列唯一值数量的较大者,用作平均每个值匹配行数的分母,以避免乘积模型在高度偏斜场景下的严重低估。
假设有三个表 emp,dept,kids:
emp:
eid
employee
1
Lee
2
Kim
3
Sam
dept:
eid
department
1
财务部
2
财务部
3
行政部
kids:
eid
name
1
Neil
1
Lebron
2
Justin
3
Tom
如果执行 SELECT * FROM emp, dept, kids WHERE eid = eid AND emp.eid = kids.eid;,也就是没有过滤条件的情况,那么
∣ e m p ∣ = 3 ∣ d e p t ∣ = 3 ∣ k i d s ∣ = 4
\lvert emp\rvert = 3 \quad \lvert dept\rvert = 3 \quad \lvert kids\rvert = 4
∣ e m p ∣ = 3 ∣ d e p t ∣ = 3 ∣ k i d s ∣ = 4 d e , e i d = 3 d d , e i d = 3 d k , e i d = 3
d_{e,\mathrm{eid}} = 3 \quad d_{d,\mathrm{eid}} = 3 \quad d_{k,\mathrm{eid}} = 3
d e , e i d = 3 d d , e i d = 3 d k , e i d = 3 ∣ e m p ⋈ d e p t ∣ ≈ 3 × 3 max ( 3 , 3 ) = 3 × 3 3 = 3
\bigl|\text{emp}\Join\text{dept}\bigr| \approx \frac{3\times3}{\max(3,3)} = \frac{3\times3}{3} = 3
∣ ∣ e m p ⋈ d e p t ∣ ∣ ≈ max ( 3 , 3 ) 3 × 3 = 3 3 × 3 = 3 ∣ e m p ⋈ k i d s ∣ ≈ 3 × 4 max ( 3 , 3 ) = 3 × 4 3 = 4
\bigl|\text{emp}\Join\text{kids}\bigr| \approx \frac{3\times4}{\max(3,3)} = \frac{3\times4}{3} = 4
∣ ∣ e m p ⋈ k i d s ∣ ∣ ≈ max ( 3 , 3 ) 3 × 4 = 3 3 × 4 = 4 ∣ ( e m p ⋈ d e p t ) ⋈ k i d s ∣ ≈ 3 × 4 max ( 3 , 3 ) = 3 × 4 3 = 4
\bigl|(\text{emp}\Join\text{dept})\Join\text{kids}\bigr| \approx \frac{3\times4}{\max(3,3)} = \frac{3\times4}{3} = 4
∣ ∣ ( e m p ⋈ d e p t ) ⋈ k i d s ∣ ∣ ≈ max ( 3 , 3 ) 3 × 4 = 3 3 × 4 = 4 ,
如果执行 SELECT * FROM emp, dept, kids WHERE dept.department = '财务部' AND emp.eid = dept.eid AND emp.eid = kids.eid;,那么
∣ e m p ∣ = 3 ∣ d e p t ∣ = 1 ∣ k i d s ∣ = 4
\lvert emp\rvert = 3 \quad \lvert dept\rvert = 1 \quad \lvert kids\rvert = 4
∣ e m p ∣ = 3 ∣ d e p t ∣ = 1 ∣ k i d s ∣ = 4 d e , e i d = 3 d d , e i d = 1 d k , e i d = 3
d_{e,\mathrm{eid}} = 3 \quad d_{d,\mathrm{eid}} = 1 \quad d_{k,\mathrm{eid}} = 3
d e , e i d = 3 d d , e i d = 1 d k , e i d = 3 ∣ e m p ⋈ d e p t ∣ ≈ 3 × 1 max ( 3 , 1 ) = 3 × 1 3 = 3
\bigl|\text{emp}\Join\text{dept}\bigr| \approx \frac{3\times1}{\max(3,1)} = \frac{3\times1}{3} = 3
∣ ∣ e m p ⋈ d e p t ∣ ∣ ≈ max ( 3 , 1 ) 3 × 1 = 3 3 × 1 = 3 ∣ e m p ⋈ k i d s ∣ ≈ 3 × 4 max ( 3 , 3 ) = 3 × 4 3 = 4
\bigl|\text{emp}\Join\text{kids}\bigr| \approx \frac{3\times4}{\max(3,3)} = \frac{3\times4}{3} = 4
∣ ∣ e m p ⋈ k i d s ∣ ∣ ≈ max ( 3 , 3 ) 3 × 4 = 3 3 × 4 = 4 ∣ ( e m p ⋈ d e p t ) ⋈ k i d s ∣ ≈ 1 × 4 max ( 1 , 3 ) = 1 × 4 3 = 1 . 3
\bigl|(\text{emp}\Join\text{dept})\Join\text{kids}\bigr| \approx \frac{1\times4}{\max(1,3)} = \frac{1\times4}{3} = 1.3
∣ ∣ ( e m p ⋈ d e p t ) ⋈ k i d s ∣ ∣ ≈ max ( 1 , 3 ) 1 × 4 = 3 1 × 4 = 1 . 3 。
思考:
这里出现小数点有影响么?
实际上是没有影响的,这个指标只用于基数评估并最终用于确定执行计划,实际的操作执行和这个无关。
基数的低估和高估问题
基数估算问题可分为低估(Under-Estimates)和高估(Over-Estimates)两类。两者均会导致选错执行计划,但低估往往更具破坏性 :当优化器低估中间结果行数时,可能选择内存嵌套循环而不是外部哈希连接,导致大量磁盘溢写和 I/O 阻塞,从而极度拖慢查询。独立性假设是导致低估的主要根源之一,因为真实数据中列间高度相关时,简单的乘积模型会大幅低估联合选择性。